Homogenisation

This was the focus of the first chapter in my thesis. In collaboration with my advisor J.I. Diaz, Prof Tatiana Shaposhnikova and Drs A.V. Podolskii and M.N. Zubova from Moscow State University, we studied reaction diffusion problems in periodically perforated domains.

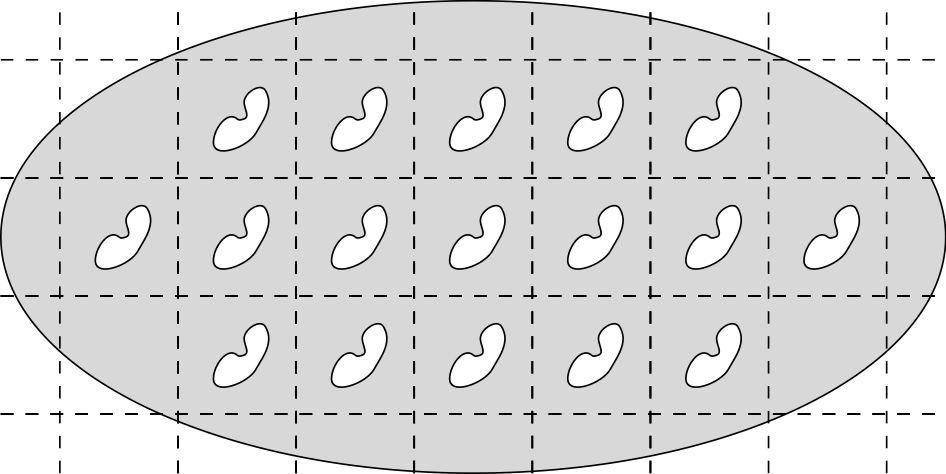
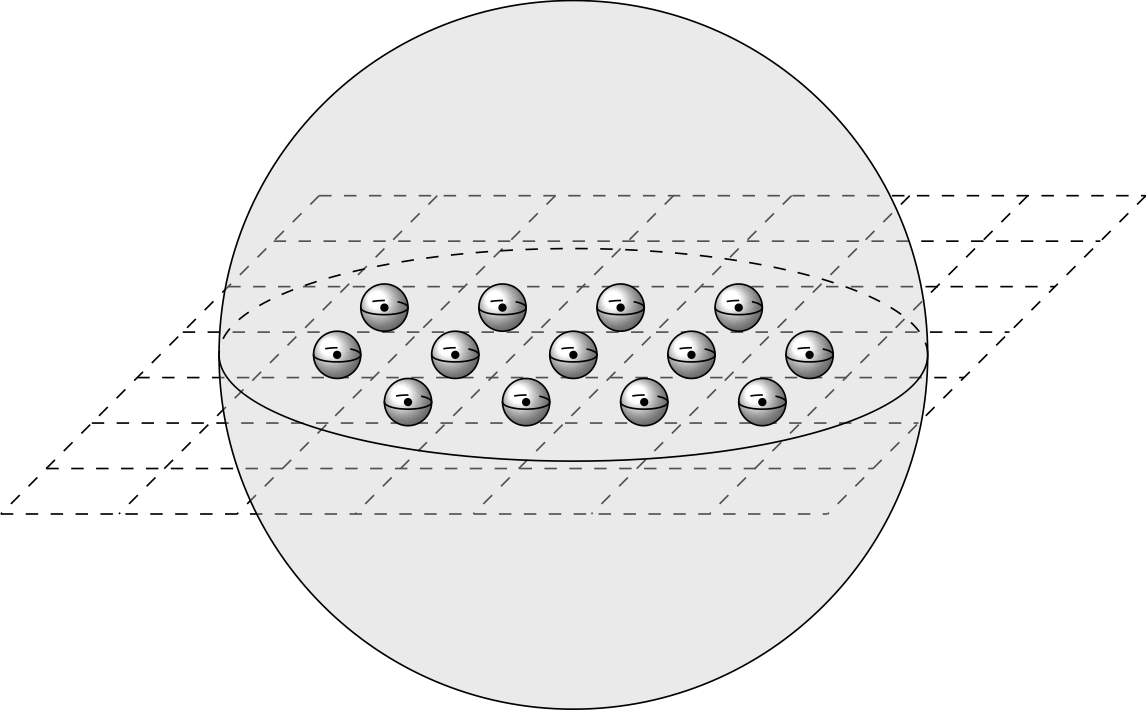
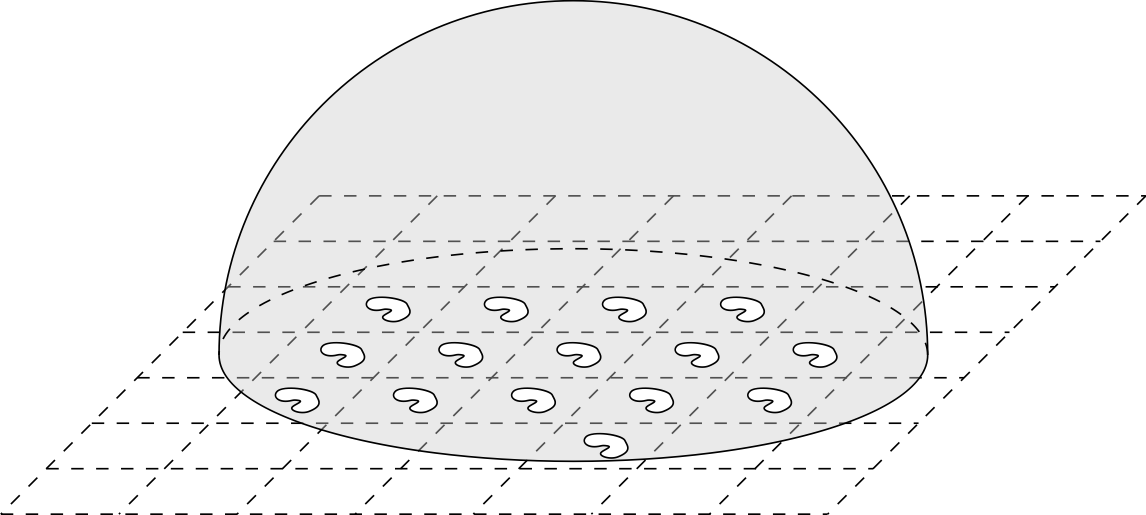
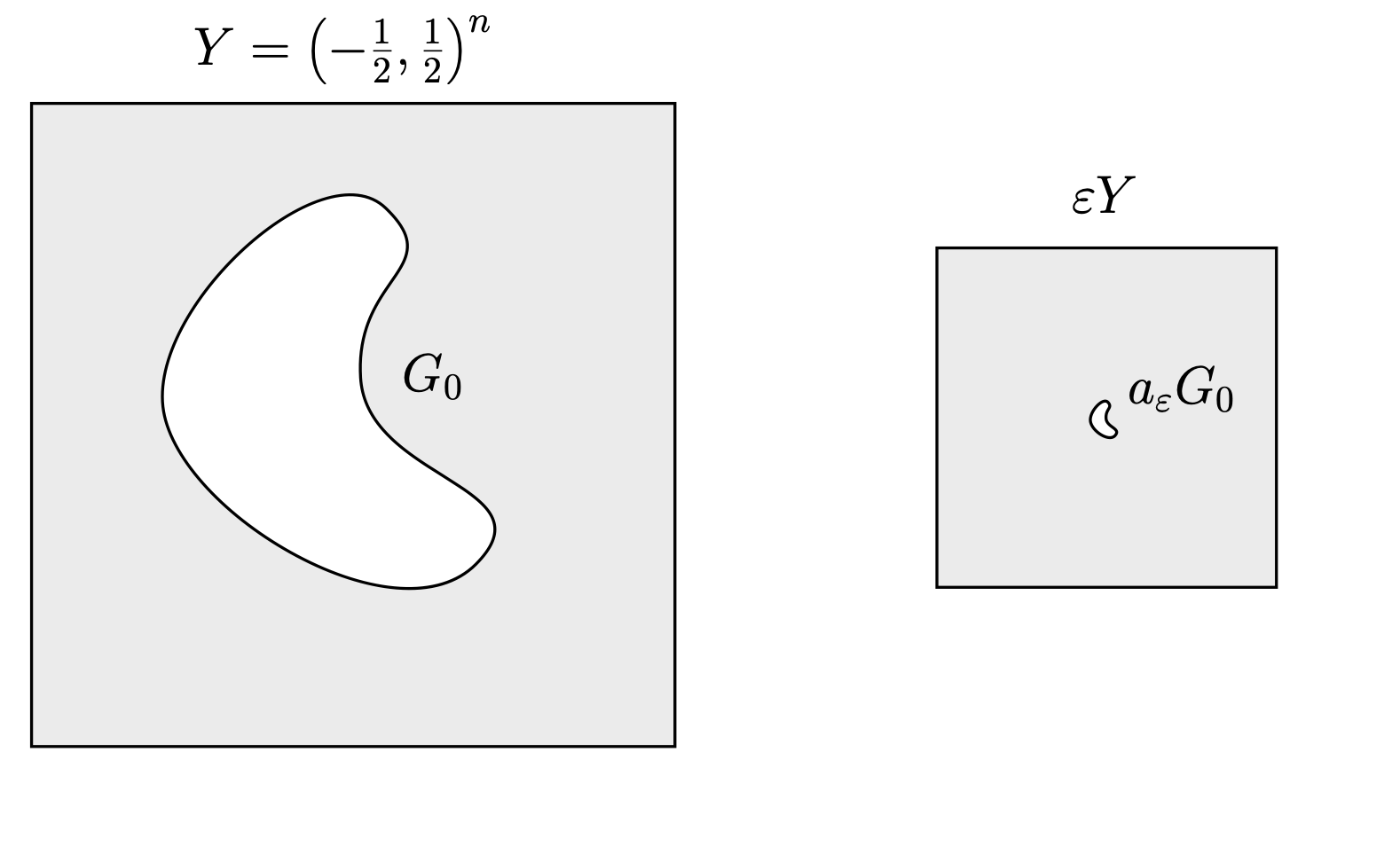
The particles are always considered to be at distance $\varepsilon$, whereas the size of the particles are allowed to $ a_\varepsilon $. This scaling parameter is typically chosen as $a_\varepsilon = C_0 \varepsilon^\alpha $ with $\alpha \ge 1$.

This problem is relevant in Chemical Engineering, and has been studied my a number of prominent mathematicians as, for example, Olga Oleinik. The objective is to characterise the effective behaviour of the solutions as $ \varepsilon$ tends to $0$, where particles are no longer present. There exists a critical scale $a_ \varepsilon$, where the nature of the limit problem changes. This property (first noticed by D. Cioranescu and F. Murat) is related to the surprising properties of nano-materials.

Through a systematic study of these problems, we have been able to extend the theory to very general classes of non-linear reactions (maximal monotone graphs instead of differentiable functions) and to general shapes of particles (the Neumann case was only understood for balls).

As a summit of this research line, we present the complete theory in the book [Díaz, Gómez-Castro & Shaposhnikova, 2021]. We published more than 10 papers on the subject: [Díaz, Gómez-Castro, Podol’skii & Shaposhnikova, 2016; Díaz, Gómez-Castro, Podol’skii & Shaposhnikova, 2017; Díaz, Gómez-Castro, Podolskii & Shaposhnikova, 2017; Díaz, Gómez-Castro, Podol’skii & Shaposhnikova, 2019; Díaz, Gómez-Castro, Podolskii & Shaposhnikova, 2018; Díaz, Gómez-Castro, Shaposhnikova & Zubova, 2019; Díaz, Gómez-Castro, Shaposhnikova & Zubova, 2017; Díaz & Gómez-Castro, 2017; Díaz, Gómez-Castro, Shaposhnikova & Zubova, 2019; Díaz, Gómez-Castro, Shaposhnikova & Zubova, 2020; Díaz, Gómez-Castro, Podolskiy & Shaposhnikova, 2018; Díaz, Gómez-Castro, Podolskiy & Shaposhnikova, 2020; Díaz, Gómez-Castro & Timofte, 2015].

References

1. Díaz, J. I. and Gómez-Castro, D. and Shaposhnikova, T. A (2021) . Nonlinear Reaction-Diffusion Processes for Nanocomposites. De Gruyter. Link
2. Díaz, J. I. and Gómez-Castro, D. and Podol’skii, A. V. and Shaposhnikova, T. A. (2016) . Homogenization of the p-Laplace operator with nonlinear boundary condition on critical size particles: identifying the strange terms for some non smooth and multivalued operators. Doklady Mathematics. Link
3. Díaz, J. I. and Gómez-Castro, D. and Podol’skii, A. V. and Shaposhnikova, T. A. (2017) . Homogenization of variational inequalities of Signorini type for the p-Laplacian in perforated domains when p ∈(1, 2). Doklady Mathematics. Link
4. Díaz, J. I. and Gómez-Castro, D. and Podolskii, A.V. and Shaposhnikova, T.A. (2017) . On the asymptotic limit of the effectiveness of reaction–diffusion equations in periodically structured media. Journal of Mathematical Analysis and Applications. Link
5. Díaz, J. I. and Gómez-Castro, D. and Podol’skii, Alexander V and Shaposhnikova, T. A (2019) . Characterizing the strange term in critical size homogenization: Quasilinear equations with a general microscopic boundary condition. Adv. Nonlinear Anal.. Link
6. Díaz, J. I. and Gómez-Castro, D. and Podolskii, A. V. and Shaposhnikova, T. A. (2018) . Non existence of critical scales in the homogenization of the problem with p-Laplace diffusion and nonlinear reaction in the boundary of periodically distributed particles in n-dimensional domains when p>n. Rev. la Real Acad. Ciencias Exactas, Físicas y Nat. Ser. A. Matemáticas. Link
7. Díaz, J. I. and Gómez-Castro, D. and Shaposhnikova, T. A. and Zubova, M. N. (2019) . Classification of homogenized limits of diffusion problems with spatially dependent reaction over critical-size particles. Appl. Anal.. Link
8. Díaz, J. I. and Gómez-Castro, D. and Shaposhnikova, T. A. and Zubova, M. N. (2017) . Change of homogenized absorption term in diffusion processes with reaction on the boundary of periodically distributed asymmetric particles of critical size. Electronic Journal of Differential Equations. Link
9. Díaz, J. I. and Gómez-Castro, D. (2017) . A mathematical proof in nanocatalysis: better homogenized results in the diffusion of a chemical reactant through critically small reactive particles. in Progress in Industrial Mathematics at ECMI 2016. Link
10. Díaz, J. I. and Gómez-Castro, D. and Shaposhnikova, T. A. and Zubova, Maria N. (2019) . A nonlocal memory strange term arising in the critical scale homogenisation of a diffusion equation with a dynamic boundary condition. Electron. J. Differ. Equ.. Link
11. Díaz, J. I. and Gómez-Castro, D. and Shaposhnikova, T. A. and Zubova, M. N. (2020) . A Time-Dependent Strange Term Arising in Homogenization of an Elliptic Problem with Rapidly Alternating Neumann and Dynamic Boundary Conditions Specified at the Domain Boundary: The Critical Case. Dokl. Math.. Link
12. Díaz, J. I. and Gómez-Castro, D. and Podolskiy, A. V. and Shaposhnikova, T. A. (2018) . Homogenization of Boundary Value Problems in Plane Domains with Frequently Alternating Type of Nonlinear Boundary Conditions: Critical Case. Dokl. Math.. Link
13. Díaz, J. I. and Gómez-Castro, D. and Podolskiy, Alexander V and Shaposhnikova, T. A (2020) . Homogenization of a net of periodic critically scaled boundary obstacles related to reverse osmosis “nano-composite” membranes. Adv. Nonlinear Anal.. Link
14. Díaz, J. I. and Gómez-Castro, D. and Timofte, Claudia (2015) . On the influence of pellet shape on the effectiveness factor of homogenized chemical reactions. in Proceedings Of The XXIV Congress On Differential Equations And Applications XIV Congress On Applied Mathematics.